滚动轴承广泛应用于各类旋转机械中，行业涉及航空航天、建筑、采矿、化工、钢铁、造纸、纺织、电力、铁路等国家工业命脉。旋转机械故障中约有40%来源于轴承损伤和缺陷。安装不良、维护不及时、轴承滚道表面疲劳等均可能导致轴承缺陷。严重的轴承故障如航空发动机中介轴承失稳保持架断裂、火车轮毂轴承润滑不良导致滚动体卡死等会造成重大经济损失甚至人员伤亡。轴承内外圈缺陷、滚动体缺陷、保持架失稳、轴承-转子不对中等常见故障均会在轴承座振动信号中出现明显特征。因此，基于振动分析的滚动轴承的故障预警在工程上极为重要。以下图1-图4分别为轴承中常见的几种故障类型。

图1 内圈缺陷

图2 滚道划伤

图3 保持架断裂

图4 滚动体分布式缺陷

接触疲劳是轴承各类表面缺陷形成的主要原因。它的一般特征是滚道在周期性的加载卸载动态压力下，金属颗粒从滚道上剥落，并进一步的对健康滚道产生破坏；或者在动态压力下产生滚道产生微裂纹，微裂纹在轴承运转中迅速扩展剥落形成大尺度坑状缺陷，如图5所示。裂纹通常出现在微观结构的不连续处，例如夹杂物、最大应力区的微塑性变形导致的不均匀性和碳化物簇。这就对轴承制造企业在轴承材料的研发和选择、加工精度等环节提出要求。

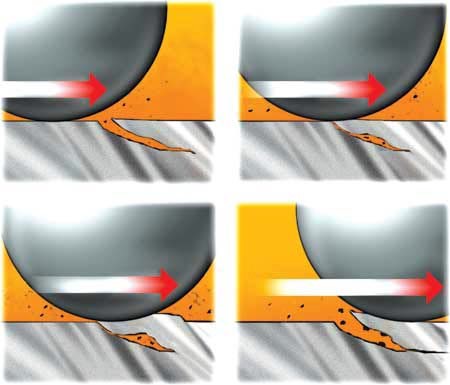
图5 轴承滚道疲劳损伤过程

基于轴承滚道及滚子的疲劳损伤提出的轴承使用寿命理论分为概率工程模型和定量研究模型。在工程应用中，基于Lundberg-Palmgren模型的Weibull分布图被广泛的应用于轴承寿命预测中。轴承的寿命概率系数S可由以下模型求得[1]：

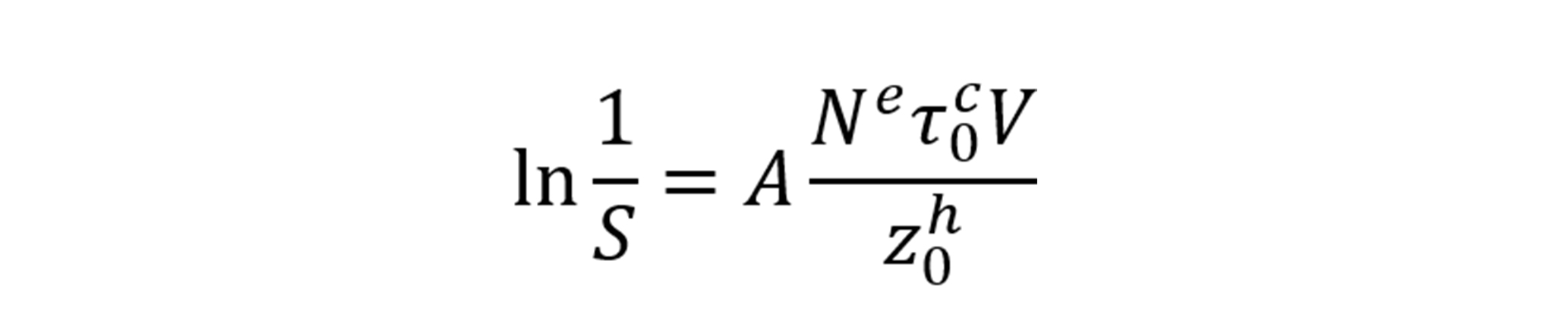
其中τ是接触区最大正交切应力，Z为对应的变形，N为轴承圈转动圈数，V为材料受力的体积，A、c、h为由实验确定的材料系数。图6为基于以上模型的1309调心轴承和6309深沟球轴承的转动圈数和寿命概率分布图。

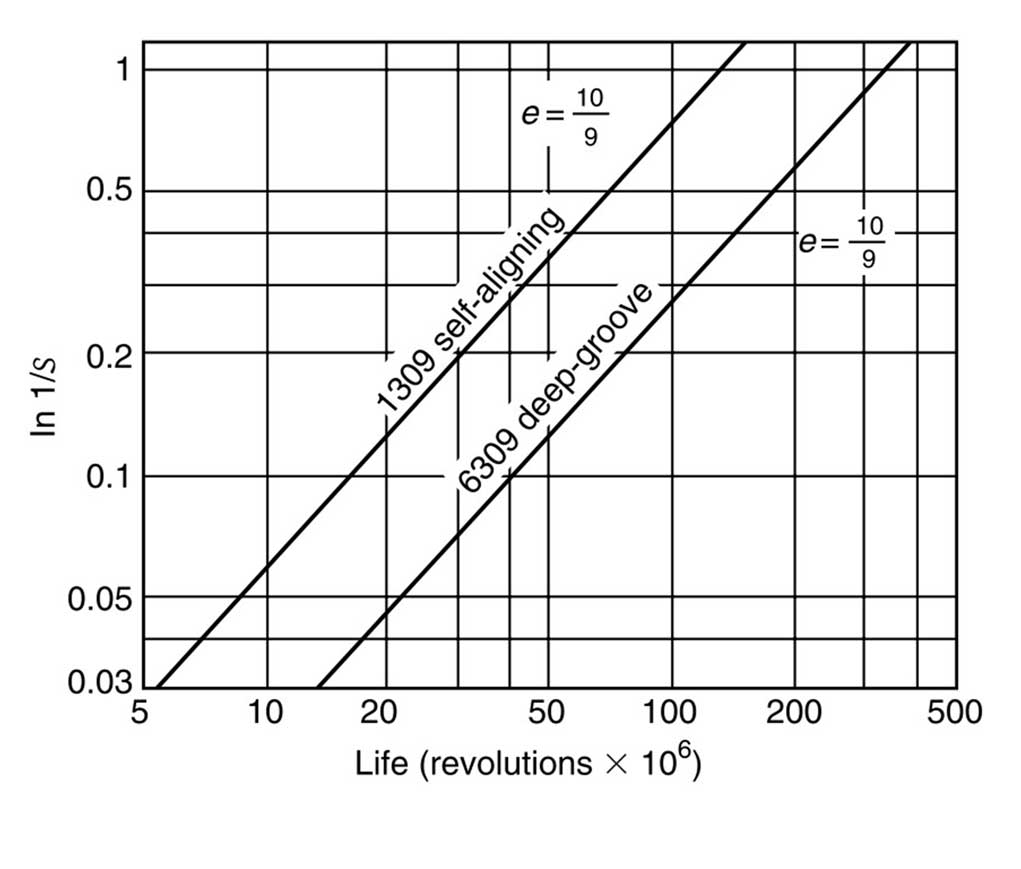
图6 寿命预测案例

轴承局部缺陷包括轴承各部件的裂纹、凹坑、剥落。研究学者对轴承局部缺陷做了广泛且系统的研究，为模拟这些故障下的振动特征，学者们提出的轴承模型可以分为以下几类[2]：

其中周期性冲击序列模型及准周期冲击序列模型不包含轴承的具体物理参数，也不引入滚动体-滚道的赫兹接触变形分析。这种简化的模型在故障频率下的幅值预测与实际情况往往不符，因此，下面着重讨论在此模型基础上发展出的非线性多体动力学模型。

基于集中参数模型的轴承的非线性多体动力学模型是由一系列弹簧连接的简化刚性质量（用于非线性接触建模）和阻尼器构成。用于模拟有局部缺陷的轴承振动特性。通常外圈-轴承座、内圈-转子之间被视为刚性连接；滚动体质量相对于外圈-轴承座组合、内圈-转子组合较小，一般不体现在非线性模型中；轴承的打滑虽然常见于各类高速轻载轴承中，但由于打滑现象的预测需考虑轴承部件的热流固耦合及润滑油的温-压-粘效应，因此也不振动预测中涉及。图7为一10自由度的角接触轴承非线性动力学模型，考虑横向，轴向以及角度偏摆方向的振动，局部缺陷为考虑周向、轴向、深度的三维缺陷[3]。图8给出了相应的五个方向的振动加速度特性，并且与滚珠落入缺陷的深度图谱做对比，可以明显的看到滚子进入缺陷区和滚出缺陷区产生的振动冲击。同时，多自由度的振动特征也为实际设备的振动信号采集方式提供选择。

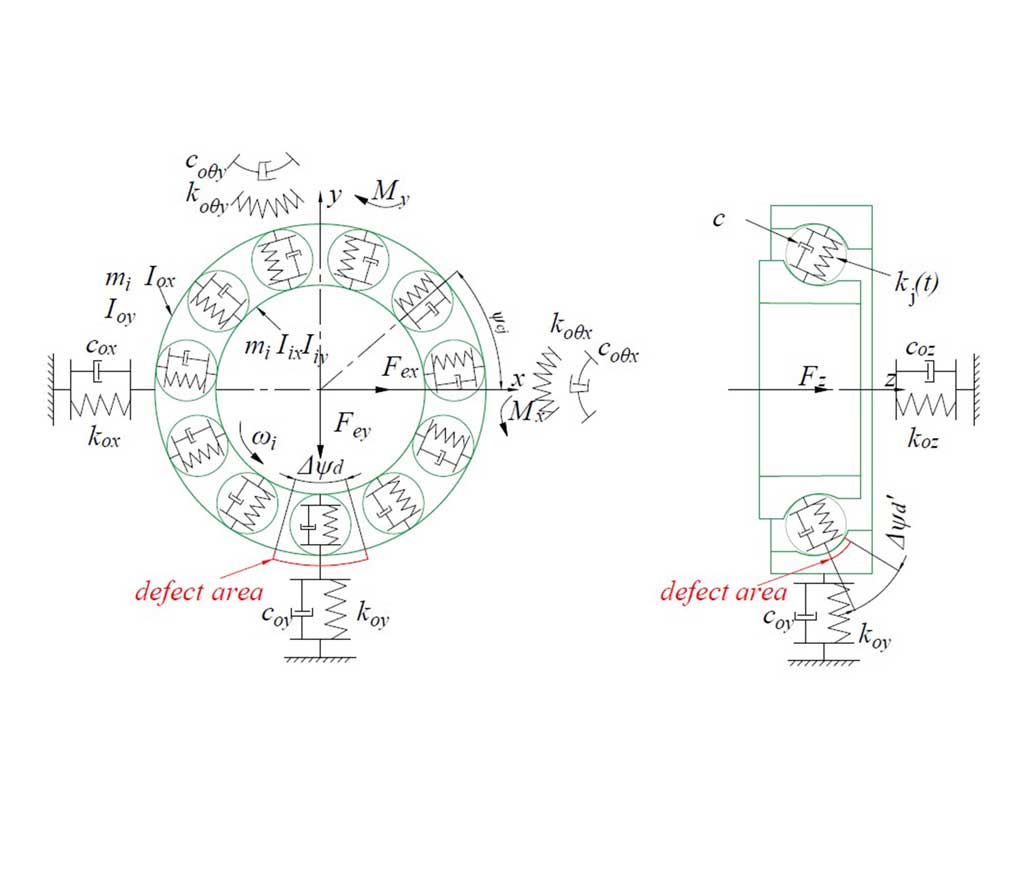
图7 角接触轴承外滚道三维缺陷的10自由度多体动力学模型

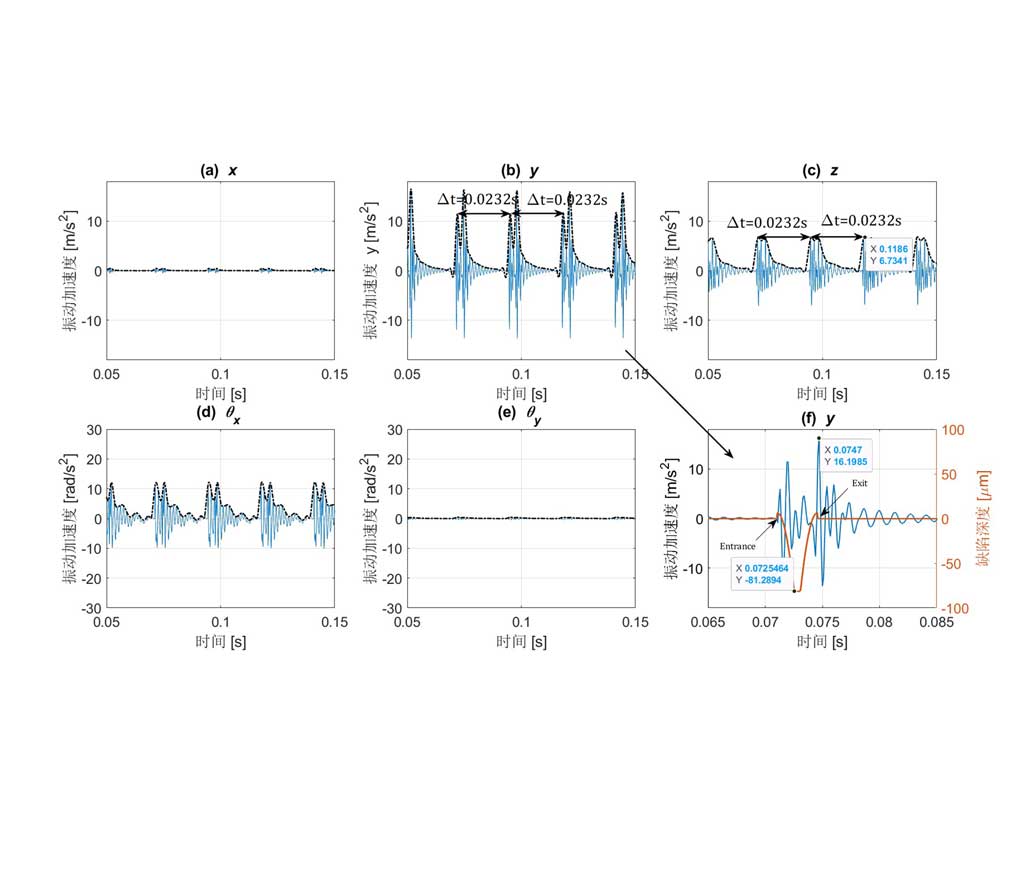
图8 外滚道三维缺陷下的各自由度振动特性与缺陷深度图谱对比

滚动体在进入缺陷时可以被看做特点不明显的低频率振动，退出缺陷则会产生高频明显的冲击。测量的加速度信号中从入口点到出口点的时间差异可以用来估计轴承缺陷的尺寸。振动幅度能够体现缺陷的严重程度。如图9为滚动体进入和退出缺陷区的瞬态响应。

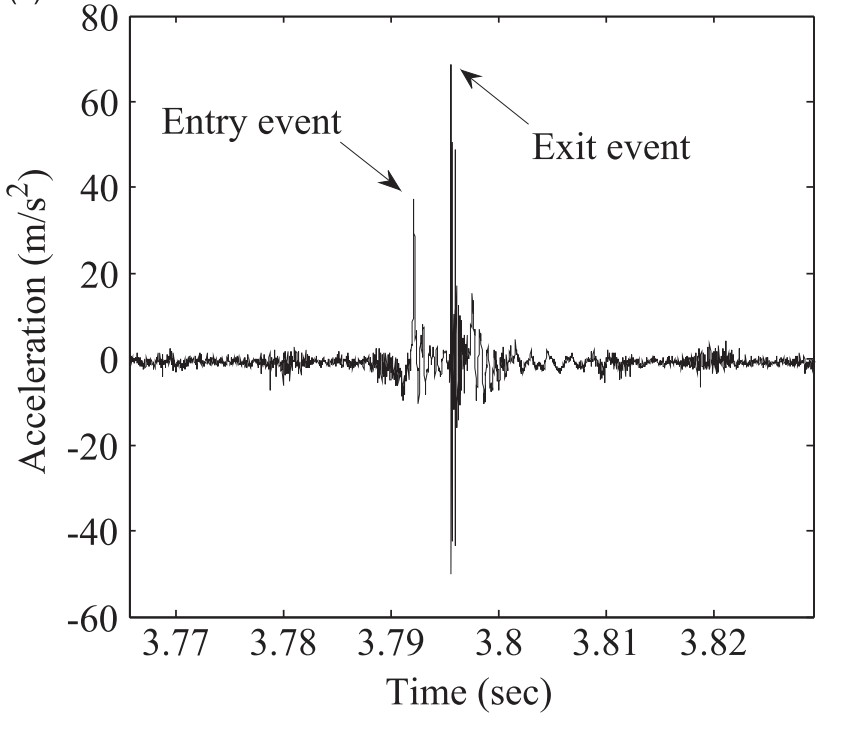
图9 滚动体进入和退出缺陷区的瞬态响应

在缺陷轴承的实测振动信号中，有学者发现滚珠进入和退出缺陷时产生双脉冲现象，即出现高频能量特征，这为以往人们认为滚珠进入缺陷为低频特征提供的补充。如图10所示[4]。

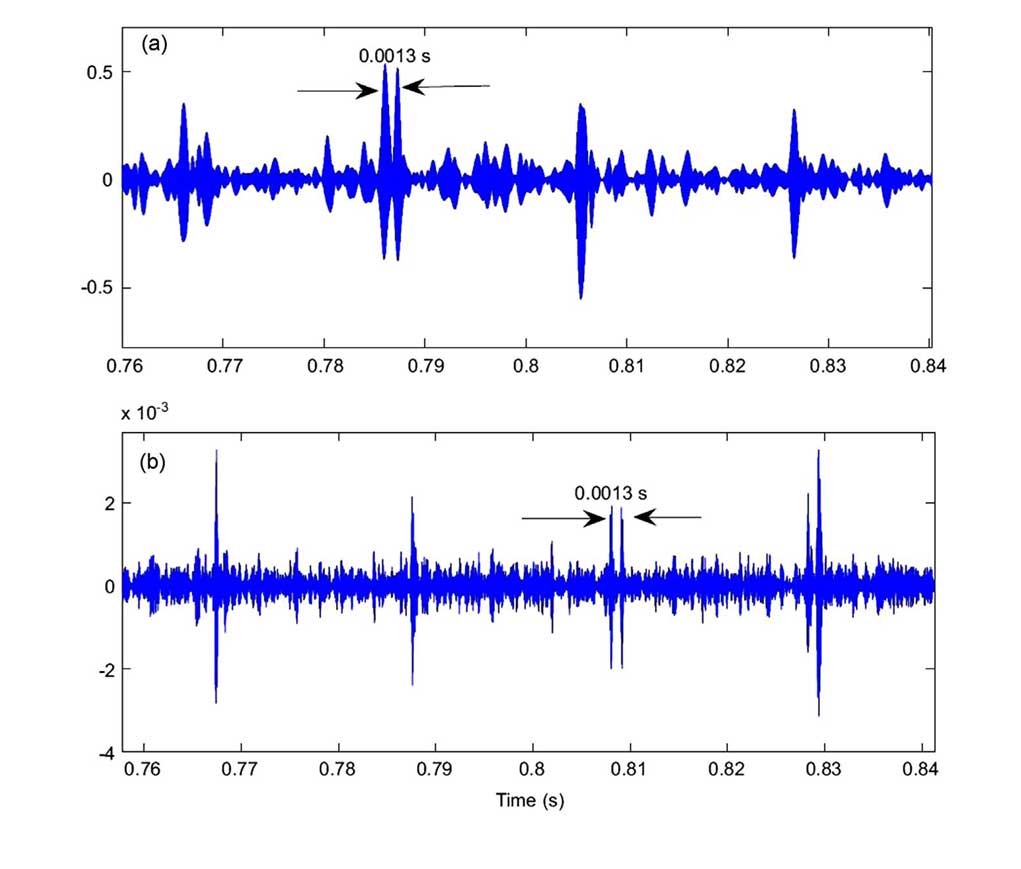
图10 双脉冲高频特征

本文将轴承故障机理，轴承振动分析模型及与缺陷相关的轴承振动特性做了简要阐述。对工程应用中关注的轴承问题做出思考。